Rozwiązanie:
6.1.2 Właściwości oczekiwań matematycznych
1. Matematyczne oczekiwanie na stałą wartość jest równe samej stałej.
2. Stały współczynnik można przyjąć jako znak oczekiwania matematycznego. ![]()
3. Oczekiwanie matematyczne iloczynu dwóch niezależnych zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych.
Ta właściwość jest prawdziwa dla dowolnej liczby zmiennych losowych.
4. Oczekiwanie matematyczne sumy dwóch zmiennych losowych jest równe sumie oczekiwań matematycznych wyrazów.
Właściwość ta jest również prawdziwa dla dowolnej liczby zmiennych losowych.
Przykład: M(X) = 5, MÓJ)= 2. Znajdź matematyczne oczekiwanie zmiennej losowej Z, stosując właściwości oczekiwań matematycznych, jeśli o tym wiadomo Z=2X+3Y.
Rozwiązanie: M(Z) = M(2X + 3Y) = M(2X) + M(3Y) = 2M(X) + 3M(Y) = 2∙5+3∙2 =
1) matematyczne oczekiwanie sumy jest równe sumie oczekiwań matematycznych
2) stały współczynnik można wyjąć ze znaku matematycznego oczekiwania
Przeprowadźmy n niezależnych prób, a prawdopodobieństwo zajścia zdarzenia A będzie równe p. Wtedy zachodzi następujące twierdzenie:
Twierdzenie. Oczekiwanie matematyczne M(X) liczby wystąpień zdarzenia A w n niezależnych próbach jest równe iloczynowi liczby prób i prawdopodobieństwa wystąpienia zdarzenia w każdej próbie.
6.1.3 Rozproszenie dyskretnej zmiennej losowej
Oczekiwanie matematyczne nie może w pełni scharakteryzować procesu losowego. Oprócz oczekiwania matematycznego należy wprowadzić wartość charakteryzującą odchylenie wartości zmiennej losowej od oczekiwania matematycznego.
Odchylenie to jest równe różnicy między zmienną losową a jej oczekiwaniem matematycznym. W tym przypadku matematyczne oczekiwanie odchylenia wynosi zero. Wyjaśnia to fakt, że niektóre możliwe odchylenia są dodatnie, inne ujemne, a w wyniku ich wzajemnego zniesienia uzyskuje się zero.
Dyspersja (rozpraszanie) dyskretnej zmiennej losowej jest oczekiwaniem matematycznym kwadratu odchylenia zmiennej losowej od jej oczekiwań matematycznych.
W praktyce ta metoda obliczania wariancji jest niewygodna, ponieważ prowadzi do uciążliwych obliczeń dla dużej liczby wartości zmiennych losowych.
Dlatego stosuje się inną metodę.
Twierdzenie. Wariancja jest równa różnicy między matematycznym oczekiwaniem kwadratu zmiennej losowej X a kwadratem jej matematycznego oczekiwania.
Dowód. Biorąc pod uwagę fakt, że oczekiwanie matematyczne M(X) i kwadrat oczekiwania matematycznego M2(X) są wielkościami stałymi, możemy zapisać:
Przykład. Znajdź wariancję dyskretnej zmiennej losowej określonej przez prawo dystrybucji.
| X | ||||
| X2 | ||||
| R | 0.2 | 0.3 | 0.1 | 0.4 |
Rozwiązanie: .
6.1.4 Właściwości dyspersyjne
1. Wariancja stałej wartości wynosi zero. .
2. Stały współczynnik można usunąć ze znaku dyspersji podnosząc go do kwadratu. ![]() .
.
3. Wariancja sumy dwóch niezależnych zmiennych losowych jest równa sumie wariancji tych zmiennych. .
4. Wariancja różnicy między dwiema niezależnymi zmiennymi losowymi jest równa sumie wariancji tych zmiennych. .
Twierdzenie. Wariancja liczby wystąpień zdarzenia A w n niezależnych próbach, w których każde prawdopodobieństwo p zajścia zdarzenia jest stałe, jest równa iloczynowi liczby prób przez prawdopodobieństwa wystąpienia i nie- wystąpienie zdarzenia w każdej próbie.
Przykład: Znajdź wariancję DSV X - liczbę wystąpień zdarzenia A w 2 niezależnych próbach, jeśli prawdopodobieństwo wystąpienia zdarzenia w tych próbach jest takie samo i wiadomo, że M(X) = 1,2.
Zastosujmy twierdzenie z rozdziału 6.1.2:
M(X) = np
M(X) = 1,2; N= 2. Znajdźmy P:
1,2 = 2∙P
P = 1,2/2
Q = 1 – P = 1 – 0,6 = 0,4
Znajdźmy wariancję korzystając ze wzoru:
D(X) = 2∙0,6∙0,4 = 0,48
6.1.5 Odchylenie standardowe dyskretnej zmiennej losowej
Odchylenie standardowe zmienna losowa X nazywana jest pierwiastkiem kwadratowym wariancji.
![]() (25)
(25)
Twierdzenie. Odchylenie standardowe sumy skończonej liczby wzajemnie niezależnych zmiennych losowych jest równe pierwiastkowi kwadratowemu z sumy kwadratów odchyleń standardowych tych zmiennych.
6.1.6 Tryb i mediana dyskretnej zmiennej losowej
Moda M o DSV nazywa się najbardziej prawdopodobną wartość zmiennej losowej (czyli wartość, która ma największe prawdopodobieństwo)
Mediana M i DSV jest wartością zmiennej losowej, która dzieli szereg rozkładów na pół. Jeżeli liczba wartości zmiennej losowej jest parzysta, wówczas medianę oblicza się jako średnią arytmetyczną dwóch średnich wartości.
Przykład: Znajdź modę i medianę DSV X:
| X | ||||
| P | 0.2 | 0.3 | 0.1 | 0.4 |
Ja = = 5,5
Postęp
1. Zapoznaj się z teoretyczną częścią tej pracy (wykłady, podręcznik).
2. Wykonaj zadanie według własnej wersji.
3. Złóż sprawozdanie z pracy.
4. Chroń swoją pracę.
2. Cel pracy.
3. Postęp prac.
4. Rozwiązanie własnej opcji.
6.4 Opcje zadań do samodzielnej pracy
Opcja 1
1. Znajdź oczekiwanie matematyczne, rozproszenie, odchylenie standardowe, modę i medianę DSV X, określone przez prawo dystrybucji.
| X | ||||
| P | 0.1 | 0.6 | 0.2 | 0.1 |
2. Znajdź oczekiwanie matematyczne zmiennej losowej Z, jeśli znane są oczekiwania matematyczne X i Y: M(X)=6, M(Y)=4, Z=5X+3Y.
3. Znajdź wariancję DSV X - liczbę wystąpień zdarzenia A w dwóch niezależnych próbach, jeżeli prawdopodobieństwa wystąpienia zdarzeń w tych próbach są takie same i wiadomo, że M (X) = 1.
4. Podano listę możliwych wartości dyskretnej zmiennej losowej X: x 1 = 1, x 2 = 2, x 3
Opcja nr 2
| X | ||||
| P | 0.3 | 0.1 | 0.2 | 0.4 |
2. Znajdź oczekiwanie matematyczne zmiennej losowej Z, jeśli znane są oczekiwania matematyczne X i Y: M(X)=5, M(Y)=8, Z=6X+2Y.
3. Znajdź wariancję DSV X - liczbę wystąpień zdarzenia A w trzech niezależnych próbach, jeżeli prawdopodobieństwa wystąpienia zdarzeń w tych próbach są takie same i wiadomo, że M (X) = 0,9.
x 1 = 1, x 2 = 2, x 3 = 4, x 4= 10, znane są także matematyczne oczekiwania tej wartości i jej kwadratu: , . Znajdź prawdopodobieństwa , , , odpowiadające możliwym wartościom , i sporządź prawo dystrybucji DSV.
Opcja nr 3
1. Znajdź matematyczne oczekiwanie, rozproszenie i odchylenie standardowe DSV X, określone przez prawo dystrybucji.
| X | ||||
| P | 0.5 | 0.1 | 0.2 | 0.3 |
2. Znajdź oczekiwanie matematyczne zmiennej losowej Z, jeśli znane są oczekiwania matematyczne X i Y: M(X)=3, M(Y)=4, Z=4X+2Y.
3. Znajdź wariancję DSV X - liczbę wystąpień zdarzenia A w czterech niezależnych próbach, jeśli prawdopodobieństwa wystąpienia zdarzeń w tych próbach są takie same i wiadomo, że M (x) = 1,2.
4. Podano listę możliwych wartości dyskretnej zmiennej losowej X: x 1 = 0, x 2 = 1, x 3 = 2, x 4= 5, znane są także matematyczne oczekiwania tej wartości i jej kwadratu: , . Znajdź prawdopodobieństwa , , , odpowiadające możliwym wartościom , i sporządź prawo dystrybucji DSV.
Opcja nr 4
1. Znajdź matematyczne oczekiwanie, rozproszenie i odchylenie standardowe DSV X, określone przez prawo dystrybucji.
Oczekiwanie i wariancja to najczęściej używane cechy liczbowe zmiennej losowej. Charakteryzują najważniejsze cechy rozkładu: jego położenie i stopień rozproszenia. W wielu praktycznych problemach pełna, wyczerpująca charakterystyka zmiennej losowej – prawo dystrybucji – albo w ogóle nie może zostać uzyskana, albo w ogóle nie jest potrzebna. W takich przypadkach ogranicza się do przybliżonego opisu zmiennej losowej za pomocą charakterystyk numerycznych.
Wartość oczekiwana jest często nazywana po prostu średnią wartością zmiennej losowej. Rozproszenie zmiennej losowej jest cechą dyspersji, rozproszenia zmiennej losowej wokół jej oczekiwań matematycznych.
Oczekiwanie dyskretnej zmiennej losowej
Przyjrzyjmy się koncepcji oczekiwań matematycznych, opierając się najpierw na mechanicznej interpretacji rozkładu dyskretnej zmiennej losowej. Niech masa jednostkowa zostanie rozłożona pomiędzy punktami osi x X1 , X 2 , ..., X N, a każdemu punktowi materialnemu odpowiada masa P1 , P 2 , ..., P N. Należy wybrać jeden punkt na osi odciętych, charakteryzujący położenie całego układu punktów materialnych, z uwzględnieniem ich mas. Naturalnym jest, że za taki punkt przyjmuje się środek masy układu punktów materialnych. Jest to średnia ważona zmiennej losowej X, do którego odcięta jest każdy punkt XI wchodzi z „wagą” równą odpowiedniemu prawdopodobieństwu. Uzyskana w ten sposób średnia wartość zmiennej losowej X nazywa się jego oczekiwaniem matematycznym.
Matematyczne oczekiwanie dyskretnej zmiennej losowej jest sumą iloczynów wszystkich jej możliwych wartości i prawdopodobieństw tych wartości:

Przykład 1. Zorganizowano loterię, w której wygrywają obie strony. Wygranych jest 1000, z czego 400 to 10 rubli. 300 - 20 rubli za sztukę. 200 - 100 rubli za sztukę. i 100 - 200 rubli za sztukę. Jaka jest średnia wygrana osoby, która kupi jeden los?
Rozwiązanie. Średnie wygrane znajdziemy, jeśli podzielimy całkowitą kwotę wygranych, która wynosi 10*400 + 20*300 + 100*200 + 200*100 = 50 000 rubli, przez 1000 (całkowita kwota wygranych). Następnie otrzymujemy 50000/1000 = 50 rubli. Jednak wyrażenie służące do obliczenia średnich wygranych można przedstawić w następującej formie:

Z drugiej strony w tych warunkach zwycięska wielkość jest zmienną losową, która może przyjmować wartości 10, 20, 100 i 200 rubli. z prawdopodobieństwem równym odpowiednio 0,4; 0,3; 0,2; 0,1. Dlatego oczekiwana średnia wygrana jest równa sumie iloczynów wielkości wygranych i prawdopodobieństwa ich otrzymania.
Przykład 2. Wydawca podjął decyzję o wydaniu nowej książki. Planuje sprzedać książkę za 280 rubli, z czego sam otrzyma 200, 50 - księgarnia i 30 - autor. Tabela zawiera informacje o kosztach wydania książki i prawdopodobieństwie sprzedaży określonej liczby egzemplarzy książki.
Znajdź oczekiwany zysk wydawcy.
Rozwiązanie. Zmienna losowa „zysk” jest równa różnicy między przychodem ze sprzedaży a kosztem kosztów. Na przykład, jeśli sprzeda się 500 egzemplarzy książki, dochód ze sprzedaży wynosi 200 * 500 = 100 000, a koszt publikacji to 225 000 rubli. Tym samym wydawcy grozi strata 125 000 rubli. Poniższa tabela podsumowuje oczekiwane wartości zmiennej losowej – zysk:
| Numer | Zysk XI | Prawdopodobieństwo PI | XI P I |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Całkowity: | 1,00 | 25000 |
Otrzymujemy w ten sposób matematyczne oczekiwanie zysku wydawcy:
![]() .
.
Przykład 3. Prawdopodobieństwo trafienia jednym strzałem P= 0,2. Określ zużycie pocisków, które zapewniają matematyczną oczekiwaną liczbę trafień równą 5.
Rozwiązanie. Z tego samego matematycznego wzoru oczekiwań, którego używaliśmy do tej pory, wyrażamy X- zużycie powłoki:
![]() .
.
Przykład 4. Określ oczekiwanie matematyczne zmiennej losowej X liczba trafień trzema strzałami, jeżeli prawdopodobieństwo trafienia przy każdym strzale P = 0,4 .
Wskazówka: znajdź prawdopodobieństwo wartości zmiennych losowych według Wzór Bernoulliego .
Właściwości oczekiwań matematycznych
Rozważmy właściwości oczekiwań matematycznych.
Właściwość 1. Matematyczne oczekiwanie na stałą wartość jest równe tej stałej:
Własność 2. Stały współczynnik można wyjąć z matematycznego znaku oczekiwania:
![]()
Własność 3. Oczekiwanie matematyczne sumy (różnicy) zmiennych losowych jest równe sumie (różnicy) ich oczekiwań matematycznych:
Właściwość 4. Oczekiwanie matematyczne iloczynu zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych:
Własność 5. Jeśli wszystkie wartości zmiennej losowej X zmniejszyć (zwiększyć) o tę samą liczbę Z, to jego oczekiwanie matematyczne zmniejszy się (zwiększy) o tę samą liczbę:
![]()
Kiedy nie możesz ograniczyć się tylko do oczekiwań matematycznych
W większości przypadków jedynie oczekiwanie matematyczne nie jest w stanie w wystarczającym stopniu scharakteryzować zmiennej losowej.
Niech zmienne losowe X I Y wynikają z następujących praw dystrybucji:
| Oznaczający X | Prawdopodobieństwo |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Oznaczający Y | Prawdopodobieństwo |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Oczekiwania matematyczne tych wielkości są takie same – równe zeru:
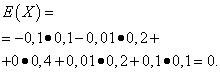
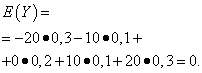
Jednak ich schematy dystrybucji są różne. Losowa wartość X może przyjmować jedynie wartości niewiele różniące się od oczekiwań matematycznych oraz zmienną losową Y może przyjmować wartości znacznie odbiegające od oczekiwań matematycznych. Podobny przykład: średnia płaca nie pozwala ocenić udziału wysoko i nisko opłacanych pracowników. Innymi słowy, na podstawie oczekiwań matematycznych nie można ocenić, jakie odchylenia od nich, przynajmniej średnio, są możliwe. Aby to zrobić, musisz znaleźć wariancję zmiennej losowej.
Wariancja dyskretnej zmiennej losowej
Zmienność Dyskretna zmienna losowa X nazywa się oczekiwaniem matematycznym kwadratu jego odchylenia od oczekiwania matematycznego:
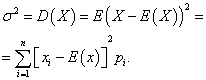
Odchylenie standardowe zmiennej losowej X wartość arytmetyczną pierwiastka kwadratowego z jej wariancji nazywa się:
![]() .
.
Przykład 5. Obliczanie wariancji i odchyleń standardowych zmiennych losowych X I Y, których prawa dystrybucji podano w tabelach powyżej.
Rozwiązanie. Matematyczne oczekiwania zmiennych losowych X I Y, jak stwierdzono powyżej, są równe zeru. Zgodnie ze wzorem dyspersji przy mi(X)=mi(y)=0 otrzymujemy:

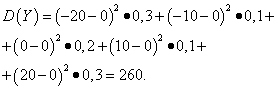
Następnie odchylenia standardowe zmiennych losowych X I Y makijaż
![]() .
.
Zatem przy tych samych oczekiwaniach matematycznych wariancja zmiennej losowej X bardzo mała, ale zmienna losowa Y- istotne. Jest to konsekwencja różnic w ich rozmieszczeniu.
Przykład 6. Inwestor posiada 4 alternatywne projekty inwestycyjne. Tabela podsumowuje oczekiwany zysk w tych projektach z odpowiednim prawdopodobieństwem.
| Projekt 1 | Projekt 2 | Projekt 3 | Projekt 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Znajdź matematyczne oczekiwanie, wariancję i odchylenie standardowe dla każdej alternatywy.
Rozwiązanie. Pokażmy, jak obliczane są te wartości dla 3. alternatywy:
Tabela podsumowuje znalezione wartości dla wszystkich alternatyw.
Wszystkie alternatywy mają te same oczekiwania matematyczne. Oznacza to, że w dłuższej perspektywie wszyscy mają takie same dochody. Odchylenie standardowe można interpretować jako miarę ryzyka – im jest ono wyższe, tym większe ryzyko inwestycji. Inwestor, który nie chce dużego ryzyka, wybierze projekt 1, ponieważ ma najmniejsze odchylenie standardowe (0). Jeżeli inwestor preferuje ryzyko i wysokie zyski w krótkim czasie, to wybierze projekt o największym odchyleniu standardowym – projekt 4.
Właściwości dyspersyjne
Przedstawmy właściwości dyspersji.
Właściwość 1. Wariancja stałej wartości wynosi zero:
Własność 2. Stały współczynnik można usunąć ze znaku dyspersji podnosząc go do kwadratu:
![]() .
.
Własność 3. Wariancja zmiennej losowej jest równa matematycznemu oczekiwaniu kwadratu tej wartości, od którego odejmuje się kwadrat matematycznego oczekiwania samej wartości:
![]() ,
,
Gdzie ![]() .
.
Właściwość 4. Wariancja sumy (różnicy) zmiennych losowych jest równa sumie (różnicy) ich wariancji:
Przykład 7. Wiadomo, że dyskretna zmienna losowa X przyjmuje tylko dwie wartości: −3 i 7. Ponadto znane jest oczekiwanie matematyczne: mi(X) = 4 . Znajdź wariancję dyskretnej zmiennej losowej.
Rozwiązanie. Oznaczmy przez P prawdopodobieństwo, z jakim zmienna losowa przyjmuje wartość X1 = −3 . Następnie prawdopodobieństwo wartości X2 = 7 będzie 1- P. Wyprowadźmy równanie na oczekiwanie matematyczne:
mi(X) = X 1 P + X 2 (1 − P) = −3P + 7(1 − P) = 4 ,
gdzie otrzymujemy prawdopodobieństwa: P= 0,3 i 1 − P = 0,7 .
Prawo rozkładu zmiennej losowej:
| X | −3 | 7 |
| P | 0,3 | 0,7 |
Wariancję tej zmiennej losowej obliczamy korzystając ze wzoru z właściwości 3 dyspersji:
D(X) = 2,7 + 34,3 − 16 = 21 .
Znajdź samodzielnie matematyczne oczekiwanie zmiennej losowej, a następnie spójrz na rozwiązanie
Przykład 8. Dyskretna zmienna losowa X przyjmuje tylko dwie wartości. Przyjmuje większą z wartości 3 z prawdopodobieństwem 0,4. Ponadto znana jest wariancja zmiennej losowej D(X) = 6 . Znajdź matematyczne oczekiwanie zmiennej losowej.
Przykład 9. W urnie jest 6 kul białych i 4 czarne. Z urny wylosowano 3 kule. Liczba białych kul wśród wylosowanych kul jest dyskretną zmienną losową X. Znajdź matematyczne oczekiwanie i wariancję tej zmiennej losowej.
Rozwiązanie. Losowa wartość X może przyjmować wartości 0, 1, 2, 3. Z odpowiednich prawdopodobieństw można obliczyć reguła mnożenia prawdopodobieństwa. Prawo rozkładu zmiennej losowej:
| X | 0 | 1 | 2 | 3 |
| P | 1/30 | 3/10 | 1/2 | 1/6 |
Stąd matematyczne oczekiwanie tej zmiennej losowej:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
Wariancja danej zmiennej losowej wynosi:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Oczekiwanie i wariancja ciągłej zmiennej losowej
W przypadku ciągłej zmiennej losowej mechaniczna interpretacja oczekiwań matematycznych zachowa to samo znaczenie: środek masy jednostki masy rozłożonej w sposób ciągły na osi x z gęstością F(X). W przeciwieństwie do dyskretnej zmiennej losowej, której argumentem jest funkcja XI zmienia się gwałtownie; w przypadku ciągłej zmiennej losowej argument zmienia się w sposób ciągły. Ale matematyczne oczekiwanie ciągłej zmiennej losowej jest również powiązane z jej średnią wartością.
Aby znaleźć matematyczne oczekiwanie i wariancję ciągłej zmiennej losowej, należy znaleźć całki oznaczone . Jeśli podana jest funkcja gęstości ciągłej zmiennej losowej, to wchodzi ona bezpośrednio do całki. Jeśli podana jest funkcja rozkładu prawdopodobieństwa, to różniczkując ją, musisz znaleźć funkcję gęstości.
Nazywa się ją średnią arytmetyczną wszystkich możliwych wartości ciągłej zmiennej losowej oczekiwanie matematyczne, oznaczone lub .
Zmienna losowa Zmienną nazywa się zmienną, która w wyniku każdego testu przyjmuje jedną nieznaną wcześniej wartość, w zależności od przyczyn losowych. Zmienne losowe oznacza się dużymi literami łacińskimi: $X,\ Y,\ Z,\ \dots $ W zależności od rodzaju zmienne losowe mogą być oddzielny I ciągły.
Dyskretna zmienna losowa- jest to zmienna losowa, której wartości mogą być nie więcej niż policzalne, to znaczy skończone lub policzalne. Przez policzalność rozumiemy, że wartości zmiennej losowej można ponumerować.
Przykład 1 . Oto przykłady dyskretnych zmiennych losowych:
a) liczba trafień w cel przy $n$ strzałach, tutaj możliwe wartości to $0,\ 1,\ \dots ,\ n$.
b) liczba emblematów upuszczonych podczas rzucania monetą, tutaj możliwe wartości to $0,\ 1,\\dots,\ n$.
c) liczba statków wchodzących na pokład (przeliczalny zbiór wartości).
d) ilość połączeń przychodzących do centrali (przeliczalny zbiór wartości).
1. Prawo rozkładu prawdopodobieństwa dyskretnej zmiennej losowej.
Dyskretna zmienna losowa $X$ może przyjmować wartości $x_1,\dots ,\ x_n$ z prawdopodobieństwem $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. Nazywa się zgodność między tymi wartościami i ich prawdopodobieństwami prawo rozkładu dyskretnej zmiennej losowej. Z reguły tę zgodność określa się za pomocą tabeli, w której w pierwszym wierszu wskazane są wartości $x_1,\dots,\ x_n$, a w drugim wierszu prawdopodobieństwa $p_1,\dots,\ p_n$ odpowiadające tym wartościom są wskazane.
$\begin(tablica)(|c|c|)
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i i p_1 i p_2 & \dots & p_n \\
\hline
\end(tablica)$
Przykład 2 . Niech zmienna losowa $X$ będzie liczbą punktów uzyskanych podczas rzucania kostką. Taka zmienna losowa $X$ może przyjmować następujące wartości: $1,\ 2,\ 3,\ 4,\ 5,\ 6$. Prawdopodobieństwa wszystkich tych wartości są równe 1/6 $. Następnie prawo rozkładu prawdopodobieństwa zmiennej losowej $X$:
$\begin(tablica)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
\hline
\end(tablica)$
Komentarz. Ponieważ w prawie rozkładu dyskretnej zmiennej losowej $X$ zdarzenia $1,\ 2,\ \dots ,\ 6$ tworzą kompletną grupę zdarzeń, to suma prawdopodobieństw musi być równa jedności, czyli $ \suma(p_i)=1$.
2. Oczekiwanie matematyczne dyskretnej zmiennej losowej.
Oczekiwanie zmiennej losowej wyznacza jego „centralne” znaczenie. Dla dyskretnej zmiennej losowej oczekiwanie matematyczne oblicza się jako sumę iloczynów wartości $x_1,\dots,\ x_n$ przez prawdopodobieństwa $p_1,\dots,\ p_n$ odpowiadające tym wartościom, czyli : $M\lewo(X\prawo)=\suma ^n_(i=1)(p_ix_i)$. W literaturze angielskiej używana jest inna notacja $E\left(X\right)$.
Właściwości oczekiwań matematycznych$M\lewo(X\prawo)$:
- $M\left(X\right)$ leży pomiędzy najmniejszą i największą wartością zmiennej losowej $X$.
- Matematyczne oczekiwanie na stałą jest równe samej stałej, tj. $M\lewo(C\prawo)=C$.
- Stały współczynnik można wyjąć ze znaku oczekiwania matematycznego: $M\left(CX\right)=CM\left(X\right)$.
- Oczekiwanie matematyczne sumy zmiennych losowych jest równe sumie ich oczekiwań matematycznych: $M\lewo(X+Y\prawo)=M\lewo(X\prawo)+M\lewo(Y\prawo)$.
- Oczekiwanie matematyczne iloczynu niezależnych zmiennych losowych jest równe iloczynowi ich oczekiwań matematycznych: $M\lewo(XY\prawo)=M\lewo(X\prawo)M\lewo(Y\prawo)$.
Przykład 3 . Znajdźmy matematyczne oczekiwanie zmiennej losowej $X$ z przykładu $2$.
$$M\left(X\right)=\sum^n_(i=1)(p_ix_i)=1\cdot ((1)\over (6))+2\cdot ((1)\over (6) )+3\cdot ((1)\ponad (6))+4\cdot ((1)\ponad (6))+5\cdot ((1)\ponad (6))+6\cdot ((1 )\ponad (6))=3,5.$$
Możemy zauważyć, że $M\left(X\right)$ leży pomiędzy najmniejszą (1$) i największą (6$) wartością zmiennej losowej $X$.
Przykład 4 . Wiadomo, że matematyczne oczekiwanie zmiennej losowej $X$ jest równe $M\left(X\right)=2$. Znajdź matematyczne oczekiwanie zmiennej losowej $3X+5$.
Korzystając z powyższych właściwości, otrzymujemy $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\ cdot 2 +5=11$.
Przykład 5 . Wiadomo, że matematyczne oczekiwanie zmiennej losowej $X$ jest równe $M\left(X\right)=4$. Znajdź matematyczne oczekiwanie zmiennej losowej $2X-9$.
Korzystając z powyższych właściwości, otrzymujemy $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\ cdot 4 -9=-1$.
3. Rozproszenie dyskretnej zmiennej losowej.
Możliwe wartości zmiennych losowych o równych oczekiwaniach matematycznych mogą różnić się rozproszeniem wokół ich wartości średnich. Przykładowo w dwóch grupach uczniów średni wynik egzaminu z teorii prawdopodobieństwa okazał się 4, ale w jednej grupie wszyscy okazali się dobrymi uczniami, a w drugiej tylko uczniowie C i wybitni. Dlatego istnieje zapotrzebowanie na charakterystykę numeryczną zmiennej losowej, która pokazywałaby rozrzut wartości zmiennej losowej wokół jej oczekiwań matematycznych. Cechą tą jest dyspersja.
Wariancja dyskretnej zmiennej losowej$X$ jest równe:
$$D\lewo(X\prawo)=\suma^n_(i=1)(p_i(\lewo(x_i-M\lewo(X\prawo)\prawo))^2).\ $$
W literaturze angielskiej używana jest notacja $V\left(X\right),\ Var\left(X\right)$. Bardzo często wariancję $D\left(X\right)$ oblicza się ze wzoru $D\left(X\right)=\sum^n_(i=1)(p_ix^2_i)-(\left(M\ lewo(X \prawo)\prawo))^2$.
Właściwości dyspersyjne$D\lewo(X\prawo)$:
- Wariancja jest zawsze większa lub równa zeru, tj. $D\lewo(X\prawo)\ge 0$.
- Wariancja stałej wynosi zero, tj. $D\lewo(C\prawo)=0$.
- Ze znaku dyspersji można odjąć stały współczynnik pod warunkiem, że jest on podniesiony do kwadratu, tj. $D\lewo(CX\prawo)=C^2D\lewo(X\prawo)$.
- Wariancja sumy niezależnych zmiennych losowych jest równa sumie ich wariancji, tj. $D\lewo(X+Y\prawo)=D\lewo(X\prawo)+D\lewo(Y\prawo)$.
- Wariancja różnicy między niezależnymi zmiennymi losowymi jest równa sumie ich wariancji, tj. $D\lewo(X-Y\prawo)=D\lewo(X\prawo)+D\lewo(Y\prawo)$.
Przykład 6 . Obliczmy wariancję zmiennej losowej $X$ z przykładu $2$.
$$D\left(X\right)=\suma^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2)=((1)\over (6))\cdot (\left(1-3,5\right))^2+((1)\over (6))\cdot (\left(2-3,5\right))^2+ \dots +( (1)\ponad (6))\cdot (\left(6-3.5\right))^2=((35)\over (12))\około 2,92,$$
Przykład 7 . Wiadomo, że wariancja zmiennej losowej $X$ jest równa $D\left(X\right)=2$. Znajdź wariancję zmiennej losowej $4X+1$.
Korzystając z powyższych właściwości, znajdujemy $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0= 16D\ w lewo(X\w prawo)=16\cdot 2=32$.
Przykład 8 . Wiadomo, że wariancja zmiennej losowej $X$ jest równa $D\left(X\right)=3$. Znajdź wariancję zmiennej losowej $3-2X$.
Korzystając z powyższych właściwości, znajdujemy $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)= 4D\ w lewo(X\w prawo)=4\cdot 3=12$.
4. Dystrybucja dyskretnej zmiennej losowej.
Sposób reprezentacji dyskretnej zmiennej losowej w postaci szeregu rozkładów nie jest jedyny i, co najważniejsze, nie jest uniwersalny, gdyż za pomocą szeregu rozkładowego nie można określić ciągłej zmiennej losowej. Istnieje inny sposób przedstawienia zmiennej losowej - funkcja rozkładu.
Funkcja dystrybucyjna zmienna losowa $X$ nazywana jest funkcją $F\left(x\right)$, która określa prawdopodobieństwo, że zmienna losowa $X$ przyjmie wartość mniejszą od pewnej ustalonej wartości $x$, czyli $F\ lewo(x\prawo )=P\lewo(X< x\right)$
Własności funkcji rozkładu:
- $0\le F\lewo(x\prawo)\le 1$.
- Prawdopodobieństwo, że zmienna losowa $X$ przyjmie wartości z przedziału $\left(\alpha ;\ \beta \right)$ jest równe różnicy pomiędzy wartościami rozkładu na końcach tego interwał: $P\lewo(\alfa< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
- $F\lewo(x\prawo)$ - niemalejące.
- $(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \prawo)=1\ )$.
Przykład 9 . Znajdźmy dystrybuantę $F\left(x\right)$ dla prawa dystrybucji dyskretnej zmiennej losowej $X$ z przykładu $2$.
$\begin(tablica)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end(tablica)$
Jeśli $x\le 1$, to oczywiście $F\left(x\right)=0$ (w tym dla $x=1$ $F\left(1\right)=P\left(X< 1\right)=0$).
Jeśli 1 dolar< x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.
Jeśli 2 dolary< x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.
Jeśli 3 dolary< x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.
Jeśli 4 dolary< x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.
Jeśli 5 dolarów< x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.
Jeśli $x > 6$, to $F\lewo(x\prawo)=P\lewo(X=1\prawo)+P\lewo(X=2\prawo)+P\lewo(X=3\prawo) +P\lewo(X=4\prawo)+P\lewo(X=5\prawo)+P\lewo(X=6\prawo)=1/6+1/6+1/6+1/6+ 1/6 + 1/6 = 1 $.
Zatem $F(x)=\lewo\(\begin(macierz)
0,\ w\ x\le 1,\\
1/6, w 1< x\le 2,\\
1/3,\ w\ 2< x\le 3,\\
1/2, w 3< x\le 4,\\
2/3,\ w\ 4< x\le 5,\\
5/6,\ w\ 4< x\le 5,\\
1,\ dla\ x > 6.
\end(macierz)\right.$
Teoria prawdopodobieństwa jest specjalną gałęzią matematyki, którą studiują wyłącznie studenci uczelni wyższych. Czy lubisz obliczenia i formuły? Nie przeraża Cię perspektywa poznania rozkładu normalnego, entropii zespołowej, oczekiwań matematycznych i rozproszenia dyskretnej zmiennej losowej? Wtedy ten temat będzie dla Ciebie bardzo interesujący. Zapoznajmy się z kilkoma najważniejszymi podstawowymi pojęciami tej dziedziny nauki.
Pamiętajmy o podstawach
Nawet jeśli pamiętasz najprostsze pojęcia teorii prawdopodobieństwa, nie zaniedbuj pierwszych akapitów artykułu. Chodzi o to, że bez jasnego zrozumienia podstaw nie będziesz w stanie pracować z formułami omówionymi poniżej.
Zachodzi więc jakieś zdarzenie losowe, jakiś eksperyment. W wyniku podejmowanych przez nas działań możemy uzyskać kilka efektów – niektóre z nich występują częściej, inne rzadziej. Prawdopodobieństwo zdarzenia to stosunek liczby rzeczywiście uzyskanych wyników jednego typu do całkowitej liczby możliwych. Dopiero znając klasyczną definicję tego pojęcia można przystąpić do badań matematycznych oczekiwań i rozproszenia ciągłych zmiennych losowych.
Przeciętny
Jeszcze w szkole, na lekcjach matematyki, zacząłeś pracować ze średnią arytmetyczną. Pojęcie to jest szeroko stosowane w teorii prawdopodobieństwa i dlatego nie można go zignorować. Najważniejsze dla nas w tej chwili jest to, że spotkamy się z tym we wzorach na matematyczne oczekiwanie i rozproszenie zmiennej losowej.

Mamy ciąg liczb i chcemy znaleźć średnią arytmetyczną. Wszystko, co jest od nas wymagane, to zsumować wszystko, co jest dostępne i podzielić przez liczbę elementów w sekwencji. Załóżmy, że mamy liczby od 1 do 9. Suma elementów będzie równa 45 i tę wartość podzielimy przez 9. Odpowiedź: - 5.
Dyspersja
Z naukowego punktu widzenia dyspersja jest średnim kwadratem odchyleń uzyskanych wartości cechy od średniej arytmetycznej. Oznacza się ją jedną dużą literą łacińską D. Co jest potrzebne do jej obliczenia? Dla każdego elementu ciągu obliczamy różnicę między istniejącą liczbą a średnią arytmetyczną i podnosimy ją do kwadratu. Będzie dokładnie tyle wartości, ile może być wyników dla wydarzenia, które rozważamy. Następnie sumujemy wszystko otrzymane i dzielimy przez liczbę elementów w sekwencji. Jeśli mamy pięć możliwych wyników, podziel je przez pięć.

Dyspersja ma również właściwości, o których należy pamiętać, aby móc je wykorzystać przy rozwiązywaniu problemów. Na przykład, gdy zmienna losowa wzrasta X razy, wariancja wzrasta X razy do kwadratu (tj. X*X). Nigdy nie jest mniejsza od zera i nie polega na przesuwaniu wartości w górę lub w dół o równe wartości. Dodatkowo w przypadku prób niezależnych wariancja sumy jest równa sumie wariancji.
Teraz zdecydowanie musimy rozważyć przykłady rozproszenia dyskretnej zmiennej losowej i oczekiwania matematycznego.
Załóżmy, że przeprowadziliśmy 21 eksperymentów i otrzymaliśmy 7 różnych wyników. Każdy z nich obserwowaliśmy odpowiednio 1, 2, 2, 3, 4, 4 i 5 razy. Ile będzie równa wariancja?
Najpierw obliczmy średnią arytmetyczną: suma elementów wynosi oczywiście 21. Podziel ją przez 7 i otrzymaj 3. Teraz odejmij 3 od każdej liczby w pierwotnej sekwencji, podnieś każdą wartość do kwadratu i dodaj wyniki. Wynik wynosi 12. Teraz wystarczy podzielić liczbę przez liczbę elementów i wydawałoby się, że to wszystko. Ale jest pewien haczyk! Omówmy to.
Zależność od liczby eksperymentów
Okazuje się, że przy obliczaniu wariancji w mianowniku może znajdować się jedna z dwóch liczb: N lub N-1. Tutaj N jest liczbą przeprowadzonych eksperymentów lub liczbą elementów w sekwencji (co w zasadzie jest tym samym). Od czego to zależy?

Jeśli liczbę testów mierzymy w setkach, wówczas musimy umieścić N w mianowniku. Jeśli w jednostkach, to N-1. Naukowcy postanowili wyznaczyć granicę dość symbolicznie: dziś przechodzi ona przez liczbę 30. Jeśli przeprowadziliśmy mniej niż 30 eksperymentów, to liczbę podzielimy przez N-1, a jeśli więcej, to przez N.
Zadanie
Wróćmy do naszego przykładu rozwiązania problemu wariancji i oczekiwań matematycznych. Otrzymaliśmy liczbę pośrednią 12, którą należało podzielić przez N lub N-1. Ponieważ przeprowadziliśmy 21 eksperymentów, czyli niecałe 30, wybierzemy drugą opcję. Zatem odpowiedź brzmi: wariancja wynosi 12/2 = 2.
Wartość oczekiwana
Przejdźmy do drugiej koncepcji, którą musimy rozważyć w tym artykule. Oczekiwanie matematyczne jest wynikiem dodania wszystkich możliwych wyników pomnożonych przez odpowiednie prawdopodobieństwa. Ważne jest, aby zrozumieć, że uzyskaną wartość, a także wynik obliczenia wariancji, uzyskuje się tylko raz dla całego problemu, niezależnie od tego, ile wyników jest w nim uwzględnianych.

Wzór na oczekiwanie matematyczne jest dość prosty: bierzemy wynik, mnożymy go przez prawdopodobieństwo, dodajemy to samo dla drugiego, trzeciego wyniku itd. Wszystko, co się z tym wiąże, nie jest trudne do obliczenia. Na przykład suma wartości oczekiwanych jest równa oczekiwanej wartości sumy. To samo tyczy się pracy. Nie każda wielkość w teorii prawdopodobieństwa pozwala na wykonanie tak prostych operacji. Weźmy problem i obliczmy znaczenie dwóch pojęć, które badaliśmy jednocześnie. Poza tym oderwała nas teoria – czas na praktykę.
Jeszcze jeden przykład
Przeprowadziliśmy 50 prób i otrzymaliśmy 10 rodzajów wyników – liczby od 0 do 9 – występujące w różnych procentach. Są to odpowiednio: 2%, 10%, 4%, 14%, 2%,18%, 6%, 16%, 10%, 18%. Przypomnijmy, że aby uzyskać prawdopodobieństwa, należy podzielić wartości procentowe przez 100. W ten sposób otrzymujemy 0,02; 0,1 itd. Przedstawmy przykład rozwiązania problemu wariancji zmiennej losowej i oczekiwania matematycznego.
Średnią arytmetyczną obliczamy korzystając ze wzoru, który pamiętamy z podstawówki: 50/10 = 5.
Przeliczmy teraz prawdopodobieństwa na liczbę wyników „w kawałkach”, aby ułatwić policzenie. Otrzymujemy 1, 5, 2, 7, 1, 9, 3, 8, 5 i 9. Od każdej uzyskanej wartości odejmujemy średnią arytmetyczną, po czym podwyższamy każdy uzyskany wynik do kwadratu. Zobacz jak to zrobić na przykładzie pierwszego elementu: 1 - 5 = (-4). Dalej: (-4) * (-4) = 16. W przypadku innych wartości wykonaj te operacje samodzielnie. Jeśli zrobiłeś wszystko poprawnie, to po zsumowaniu ich wszystkich otrzymasz 90.

Kontynuujmy obliczanie wariancji i wartości oczekiwanej, dzieląc 90 przez N. Dlaczego wybieramy N, a nie N-1? Poprawnie, bo liczba przeprowadzonych eksperymentów przekracza 30. Zatem: 90/10 = 9. Mamy wariancję. Jeśli otrzymasz inny numer, nie rozpaczaj. Najprawdopodobniej popełniłeś prosty błąd w obliczeniach. Sprawdź dokładnie to, co napisałeś, a prawdopodobnie wszystko się ułoży.
Na koniec pamiętajmy o wzorze na oczekiwanie matematyczne. Nie podamy wszystkich obliczeń, napiszemy jedynie odpowiedź, którą będziesz mógł sprawdzić po wykonaniu wszystkich wymaganych procedur. Oczekiwana wartość wyniesie 5,48. Przypomnijmy tylko jak przeprowadzać operacje, używając pierwszych elementów jako przykładu: 0*0,02 + 1*0,1... i tak dalej. Jak widać, po prostu mnożymy wartość wyniku przez jego prawdopodobieństwo.
Odchylenie
Innym pojęciem ściśle związanym z dyspersją i oczekiwaniami matematycznymi jest odchylenie standardowe. Oznacza się go albo łacińskimi literami sd, albo grecką małą literą „sigma”. Koncepcja ta pokazuje, jak średnio wartości odbiegają od cechy centralnej. Aby znaleźć jego wartość, musisz obliczyć pierwiastek kwadratowy wariancji.

Jeśli narysujesz wykres rozkładu normalnego i chcesz bezpośrednio zobaczyć na nim kwadratowe odchylenie, możesz to zrobić w kilku etapach. Weź połowę obrazu na lewo lub na prawo od trybu (wartość środkowa), narysuj prostopadłą do osi poziomej, tak aby pola powstałych figur były równe. Rozmiar odcinka pomiędzy środkiem rozkładu a wynikowym rzutem na oś poziomą będzie reprezentował odchylenie standardowe.
Oprogramowanie
Jak widać z opisów wzorów i przedstawionych przykładów, obliczenie wariancji i oczekiwań matematycznych nie jest procedurą najprostszą z arytmetycznego punktu widzenia. Aby nie tracić czasu, warto skorzystać z programu stosowanego w szkołach wyższych - nazywa się to „R”. Posiada funkcje, które pozwalają obliczyć wartości dla wielu pojęć ze statystyki i teorii prawdopodobieństwa.
Na przykład określasz wektor wartości. Odbywa się to w następujący sposób: wektor<-c(1,5,2…). Теперь, когда вам потребуется посчитать какие-либо значения для этого вектора, вы пишете функцию и задаете его в качестве аргумента. Для нахождения дисперсии вам нужно будет использовать функцию var. Пример её использования: var(vector). Далее вы просто нажимаете «ввод» и получаете результат.
Wreszcie
Rozproszenie i oczekiwanie matematyczne to bez czego trudno cokolwiek w przyszłości policzyć. W głównym toku wykładów na uczelniach poruszane są one już w pierwszych miesiącach studiowania przedmiotu. To właśnie z powodu braku zrozumienia tych prostych pojęć i nieumiejętności ich obliczenia, wielu studentów od razu zaczyna mieć zaległości w programie, a później na koniec sesji otrzymuje złe oceny, co pozbawia ich stypendiów.
Ćwicz przynajmniej tydzień, pół godziny dziennie, rozwiązując zadania podobne do tych przedstawionych w tym artykule. Wtedy na dowolnym teście z teorii prawdopodobieństwa będziesz w stanie poradzić sobie z przykładami bez zbędnych wskazówek i ściągawek.
Każda indywidualna wartość jest całkowicie zdeterminowana przez jej funkcję rozkładu. Również do rozwiązywania problemów praktycznych wystarczy znajomość kilku charakterystyk numerycznych, dzięki czemu możliwe staje się przedstawienie w krótkiej formie głównych cech zmiennej losowej.
Ilości te obejmują przede wszystkim wartość oczekiwana I dyspersja .
Wartość oczekiwana— średnia wartość zmiennej losowej w teorii prawdopodobieństwa. Oznaczone jako .
Najprościej mówiąc, matematyczne oczekiwanie zmiennej losowej X(w), znajdź jak całkaLebesgue'a w odniesieniu do miary prawdopodobieństwa R oryginalny przestrzeń prawdopodobieństwa![]()
Można również znaleźć matematyczne oczekiwanie wartości jako Całka Lebesgue’a z X poprzez rozkład prawdopodobieństwa RX wielkie ilości X:
![]()
gdzie jest zbiorem wszystkich możliwych wartości X.
Matematyczne oczekiwanie funkcji od zmiennej losowej X znalezione poprzez dystrybucję RX. Na przykład, Jeśli X- zmienna losowa o wartościach w i k(x)- jednoznaczne Borelafunkcjonować X , To:
Jeśli F(x)- funkcja dystrybucyjna X, to oczekiwanie matematyczne jest reprezentowalne całkaLebesgue – Stieltjes (lub Riemann – Stieltjes):
![]()
w tym przypadku całkowalność X Pod względem ( * ) odpowiada skończoności całki
![]()
W konkretnych przypadkach, jeśli X ma rozkład dyskretny z wartościami prawdopodobnymi x k, k=1, 2, . , a następnie prawdopodobieństwa
![]()
Jeśli X ma rozkład absolutnie ciągły z gęstością prawdopodobieństwa p(x), To
![]()
w tym przypadku istnienie oczekiwania matematycznego jest równoznaczne z absolutną zbieżnością odpowiedniego szeregu lub całki.
Własności oczekiwań matematycznych zmiennej losowej.
- Matematyczne oczekiwanie stałej wartości jest równe tej wartości:
C- stała;
- M=C.M[X]
- Oczekiwanie matematyczne sumy losowo wybranych wartości jest równe sumie ich oczekiwań matematycznych:
![]()
- Oczekiwanie matematyczne iloczynu niezależnych zmiennych losowo wybranych = iloczyn ich oczekiwań matematycznych:
M=M[X]+M[Y]
Jeśli X I Y niezależny.
jeśli szereg jest zbieżny:
![]()
Algorytm obliczania oczekiwań matematycznych.
Właściwości dyskretnych zmiennych losowych: wszystkie ich wartości można przenumerować liczbami naturalnymi; przypisz każdej wartości niezerowe prawdopodobieństwo.
1. Pomnóż pary jeden po drugim: x ja NA Liczba Pi.
2. Dodaj iloczyn każdej pary x i p ja.
Na przykład, Dla N = 4 :
Funkcja rozkładu dyskretnej zmiennej losowej stopniowo wzrasta gwałtownie w tych punktach, których prawdopodobieństwa mają znak dodatni.
Przykład: Znajdź oczekiwanie matematyczne, korzystając ze wzoru.



